座標変換
・sin,cosについて
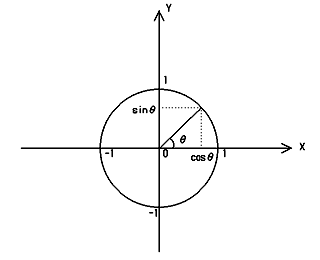
角度θがあるとします。ここでいう角度とは反時計回りならば正の値
時計回りならば負の値とします。X軸に対してθの角度をなしている
直線を考えます。この直線と半径1の円が交差している点のX座標の値が
cosθ、Y座標の値がsinθとなります。
 ・一次変換
(x,y)の点を反時計回りにθだけ回転させる場合(回転後の点は(x',y'))
x' = x * cosθ - y * sinθ
y' = x * sinθ + y * cosθ
これを行列表現にすると
|x'| = | cosθ -sinθ ||x|
|y'| | sinθ cosθ ||y|
以下概念図
・一次変換
(x,y)の点を反時計回りにθだけ回転させる場合(回転後の点は(x',y'))
x' = x * cosθ - y * sinθ
y' = x * sinθ + y * cosθ
これを行列表現にすると
|x'| = | cosθ -sinθ ||x|
|y'| | sinθ cosθ ||y|
以下概念図
 |x0' y0'| = x0 * ix + y0 * iy
|x0' y0'| = |x0 y0||cosθ sinθ|
|-sinθ cosθ|
・3次元の座標変換
|x0' y0'| = x0 * ix + y0 * iy
|x0' y0'| = |x0 y0||cosθ sinθ|
|-sinθ cosθ|
・3次元の座標変換
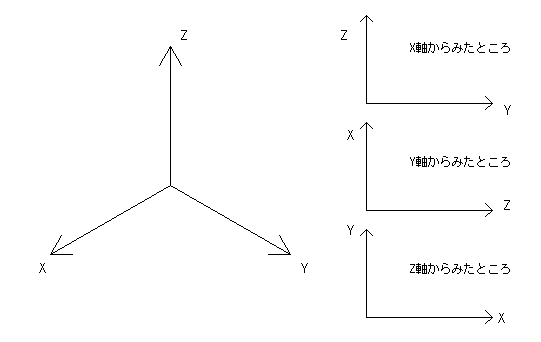 x,y,z:変換前の座標;
x',y',z':変換後の座標;
θ:回転する角度;
lx,ly,lz:平行移動量;
X軸に関する回転
|1 0 0 0|
|0 cosθ sinθ 0|
[x' y' z' 1] = [x y z 1]|0 -sinθ cosθ 0|
|0 0 0 1|
Y軸に関する回転
|cosθ 0 -sinθ 0|
|0 1 0 0|
[x' y' z' 1] = [x y z 1]|sinθ 0 cosθ 0|
|0 0 0 1|
Z軸に関する回転
|cosθ sinθ 0 0|
|-sinθ cosθ 0 0|
[x' y' z' 1] = [x y z 1]|0 0 1 0|
|0 0 0 1|
平行移動
|1 0 0 0|
|0 1 0 0|
[x' y' z' 1] = [x y z 1]|0 0 1 0|
|lx ly lz 1|
拡大縮小(スケーリング)
|sx 0 0 0|
|0 sy 0 0|
[x' y' z' 1] = [x y z 1]|0 0 sz 0|
|0 0 0 1|
これで、物体の姿勢を表現するときは
[物体の姿勢の変換行列] = [Z軸の回転行列][X軸の回転行列][Y軸の回転行列][平行移動]
|XX XY XZ 0| XX,XY,XZ・・・X軸の単位ベクトルを変換した場合のベクトル
|YX YY YZ 0| YX,YY,YZ・・・Y軸の単位ベクトルを変換した場合のベクトル
= |ZX ZY ZZ 0| ZX,ZY,ZZ・・・Z軸の単位ベクトルを変換した場合のベクトル
|LX LY LZ 1| LX,LY,LZ・・・平行移動量ベクトル
とするのが一つの方法です。この4×4行列を同次変換と呼ぶようです。
この姿勢から相対的な移動を加える場合は
[相対的な移動] = [Z軸の回転行列][X軸の回転行列][Y軸の回転行列][平行移動]
[移動後の物体の姿勢の変換行列] = [相対的な移動][移動前の物体の姿勢の変換行列]
という具合に行列の左側にどんどん変換をかけて、
頂点を変換したいなと思ったとき
[x' y' z' 1] = [x y z 1][移動後の物体の姿勢の変換行列]
としてやると便利です。
・ビューポートへの変換
ビューポートの姿勢を同次変換で表している場合は
ワールド座標からビューポート座標に変換しなければなりません
その変換は以下のようになります(スケーリングが入ってない場合)
| 1 0 0 0 || XX YX ZX 0 |
| 0 1 0 0 || XY YY ZY 0 |
[ビューポート座標系への変換] = | 0 0 1 0 || XZ YZ ZZ 0 |
| -LX -LY -LZ 1 || 0 0 0 1 |
左上の3×3行列の転置行列をとり
平行移動成分の正負を反転させたものとなります。
・関節について
x,y,z:変換前の座標;
x',y',z':変換後の座標;
θ:回転する角度;
lx,ly,lz:平行移動量;
X軸に関する回転
|1 0 0 0|
|0 cosθ sinθ 0|
[x' y' z' 1] = [x y z 1]|0 -sinθ cosθ 0|
|0 0 0 1|
Y軸に関する回転
|cosθ 0 -sinθ 0|
|0 1 0 0|
[x' y' z' 1] = [x y z 1]|sinθ 0 cosθ 0|
|0 0 0 1|
Z軸に関する回転
|cosθ sinθ 0 0|
|-sinθ cosθ 0 0|
[x' y' z' 1] = [x y z 1]|0 0 1 0|
|0 0 0 1|
平行移動
|1 0 0 0|
|0 1 0 0|
[x' y' z' 1] = [x y z 1]|0 0 1 0|
|lx ly lz 1|
拡大縮小(スケーリング)
|sx 0 0 0|
|0 sy 0 0|
[x' y' z' 1] = [x y z 1]|0 0 sz 0|
|0 0 0 1|
これで、物体の姿勢を表現するときは
[物体の姿勢の変換行列] = [Z軸の回転行列][X軸の回転行列][Y軸の回転行列][平行移動]
|XX XY XZ 0| XX,XY,XZ・・・X軸の単位ベクトルを変換した場合のベクトル
|YX YY YZ 0| YX,YY,YZ・・・Y軸の単位ベクトルを変換した場合のベクトル
= |ZX ZY ZZ 0| ZX,ZY,ZZ・・・Z軸の単位ベクトルを変換した場合のベクトル
|LX LY LZ 1| LX,LY,LZ・・・平行移動量ベクトル
とするのが一つの方法です。この4×4行列を同次変換と呼ぶようです。
この姿勢から相対的な移動を加える場合は
[相対的な移動] = [Z軸の回転行列][X軸の回転行列][Y軸の回転行列][平行移動]
[移動後の物体の姿勢の変換行列] = [相対的な移動][移動前の物体の姿勢の変換行列]
という具合に行列の左側にどんどん変換をかけて、
頂点を変換したいなと思ったとき
[x' y' z' 1] = [x y z 1][移動後の物体の姿勢の変換行列]
としてやると便利です。
・ビューポートへの変換
ビューポートの姿勢を同次変換で表している場合は
ワールド座標からビューポート座標に変換しなければなりません
その変換は以下のようになります(スケーリングが入ってない場合)
| 1 0 0 0 || XX YX ZX 0 |
| 0 1 0 0 || XY YY ZY 0 |
[ビューポート座標系への変換] = | 0 0 1 0 || XZ YZ ZZ 0 |
| -LX -LY -LZ 1 || 0 0 0 1 |
左上の3×3行列の転置行列をとり
平行移動成分の正負を反転させたものとなります。
・関節について
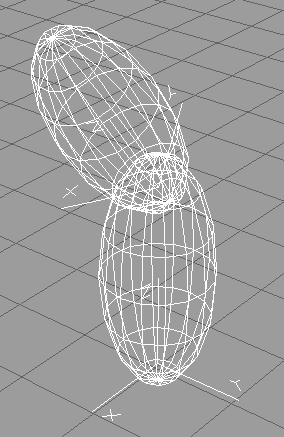 関節を表現するときの基本的な考え方は相対移動とほぼいっしょです。
[関節の変換行列] = [どれかの軸の回転行列(通常xかz?)][アームの長さ分の平行移動(通常z?)]
としておいて
[x' y' z' 1] = [x y z 1][関節の変換行列(n)][関節の変換行列(n-1)]・・・
[関節の変換行列(1)][関節の変換行列(0)]
このとき一番根元の方が[関節の変換行列(0)]で、手先の方が[関節の変換行列(n)]と
なります。また、x,y,zはn番めの関節に属する頂点です。
・透視投影
三次元の物体を二次元のスクリーンに投影することで3DCGは描かれるのですが。
その場合遠くを小さく近くのものを大きく描かれるようにする手法が
写実的な画像を描く上では一般的です。
関節を表現するときの基本的な考え方は相対移動とほぼいっしょです。
[関節の変換行列] = [どれかの軸の回転行列(通常xかz?)][アームの長さ分の平行移動(通常z?)]
としておいて
[x' y' z' 1] = [x y z 1][関節の変換行列(n)][関節の変換行列(n-1)]・・・
[関節の変換行列(1)][関節の変換行列(0)]
このとき一番根元の方が[関節の変換行列(0)]で、手先の方が[関節の変換行列(n)]と
なります。また、x,y,zはn番めの関節に属する頂点です。
・透視投影
三次元の物体を二次元のスクリーンに投影することで3DCGは描かれるのですが。
その場合遠くを小さく近くのものを大きく描かれるようにする手法が
写実的な画像を描く上では一般的です。
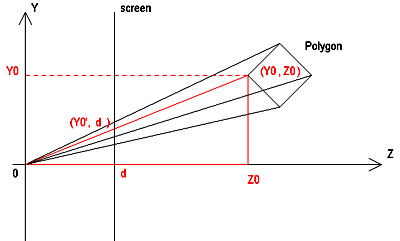 三次元のポリゴンの頂点を二次元のスクリーンに投影して
その投影された頂点を結んで2次元の多角形を描く方法をとるならば
変換をする対象は頂点ということになります。
実際に頂点の変換について考えてみます。
(X0, Y0, Z0)の点を視点からの距離dのところにあるスクリーンに投影します。
投影された後の点は(X0', Y0')とします。
これは三角形の相似から
X0' = X0 * d / Z0
Y0' = Y0 * d / Z0
となります。
三次元のポリゴンの頂点を二次元のスクリーンに投影して
その投影された頂点を結んで2次元の多角形を描く方法をとるならば
変換をする対象は頂点ということになります。
実際に頂点の変換について考えてみます。
(X0, Y0, Z0)の点を視点からの距離dのところにあるスクリーンに投影します。
投影された後の点は(X0', Y0')とします。
これは三角形の相似から
X0' = X0 * d / Z0
Y0' = Y0 * d / Z0
となります。
|